基于博弈论的TOPSIS 模型的水资源配置方案综合评价
邵 莉
On Comprehensive Evaluation of Water Resources Allocation Scheme Based on TOPSIS Model
of Game Theory
SHAO Li
文章导航 |
《437ccm必赢国际首页欢迎您学报》2023年第35卷第3期,1-6页;2023, v.35;No.136(03) 1-6 |
引用本文 |
邵莉.基于博弈论的TOPSIS模型的水资源配置方案综合评价[J].437ccm必赢国际首页欢迎您学报,2023(3):1-6 |
中图分类号 |
TV213.4 |
文献标识码 |
A Doi:10.13681/j.cnki.cn41-1282/tv.2023.03.001 |
专题 |
资源科学; 水利水电工程 |
摘要 |
科学、合理地评价水资源配置方案,对实现水资源高效利用以及解决水资源短缺具有重要意义。在熵权法与变异系数法赋权的基础上,采用博弈论思想,构建了博弈论组合赋权的TOPSIS评价模型。应用该模型对某地区水资源配置方案进行评价,并将其结果与其他模型进行对比,结果表明:该模型在水资源配置方案评价中是有效可行的,评价结果是科学的、可靠的、合理的。 |
关键词 |
水资源配置方案; 综合评价; 博弈论; TOPSIS模型; 熵权法; 变异系数法; 组合权重; |
作者介绍 |
邵莉,女,河南南阳人,河南灵捷水利勘测设计研究有限公司助理工程师,硕士,主要从事水文水资源规划、水利工程设计工作。 |
【全文获取】 |
|
 全文阅读
全文阅读
基于博弈论的TOPSIS 模型的水资源配置方案综合评价
邵 莉
(河南灵捷水利勘测设计研究有限公司,河南 南阳 510611)
摘 要:科学、合理地评价水资源配置方案,对实现水资源高效利用以及解决水资源短缺具有重要意义。在熵权法与变异系数法赋权的基础上,采用博弈论思想,构建了博弈论组合赋权的TOPSIS评价模型。应用该模型对某地区水资源配置方案进行评价,并将其结果与其他模型进行对比,结果表明:该模型在水资源配置方案评价中是有效可行的,评价结果是科学的、可靠的、合理的。
关键词:水资源配置方案;综合评价;博弈论;TOPSIS 模型;熵权法;变异系数法;组合权重
On Comprehensive Evaluation of Water Resources Allocation Scheme Based on TOPSIS Model of Game Theory
SHAO Li
(Lingjie Water Conservancy Survey & Design Research Co.,Ltd of Henan,Nanyang 510611,Henan,China)
Abstract: Scientific and reasonable evaluation of water resources allocation is of great significance for realizing efficient utilization of water resources and solving water shortage.Based on the entropy weight method and the variable coefficient method,by using the thought of Game Theory,the TOPSIS evaluation model of the combination weight of Game Theory is constructed.This model is used to evaluate the water resources allocation scheme in a certain area.The evaluation results are compared with other models’results.The results show that the model is effective and feasible in the evaluation of water resources allocation scheme,and the evaluation results are scientific,reliable and reasonable.
Key Words: Water resources allocation scheme;comprehensive evaluation;Game Theory;TOPSIS model;entropy weight method;variable coefficient method;combination weight
0 引言
水资源是重要的自然资源之一,是人类赖以生存的重要物质基础,具有不可代替性。我国水资源总量比较丰富,但人均、耕地亩均占有量较少,且时空分布不均。随着经济社会的发展和人口数量的增加,区域水资源的供需矛盾逐渐突出,水资源短缺问题已成为制约我国经济社会快速发展的问题之一。为缓解水资源供需矛盾,达到不同区域、不同用水户之间水资源的合理分配,需要制订水资源配置方案。为在众多水资源配置方案中选取最具有针对性、合理性和可持续性的水资源配置方案,需要建立水资源配置方案评价模型,对多个水资源配置方案进行评价[1-2]。
水资源配置方案评价是从水资源可持续利用的角度考虑,运用不同的评价方法,对多个水资源配置方案进行评价。根据评价结果以及项目区实际情况,可选取相对最优的水资源配置方案。目前,常用的水资源配置方案评价方法有集对分析法、模糊物元评价法、可变模糊模型、TOPSIS 模型等[3-5]。TOPSIS 评价模型是根据多个目标与理想化目标之间的贴近程度,选取相对最优的水资源配置方案。相对于其他评价方法,TOPSIS 法对评价数据没有限制,具有可操作性强、评价结果清晰明了等特点,因此经常应用于水资源配置方案评价中。在以往的水资源配置方案评价中,常采用单一赋权法,如张成凤等采用层次分析法与区间数相结合的方法确定指标权重[6];曾国熙等通过熵值法与多维递阶评价方法相结合对黑河流域水资源配置方案进行评价[7]。由于层次分析法计算得到的权重人为主观性较强,而熵值法计算得到的权重过于均衡化,采用单一赋权法的计算结果均不能完全反映评价样本的实际情况。笔者在参考以往研究成果的基础上,引入博弈论组合赋权的思想,采用TOPSIS 法构建博弈论组合赋权TOPSIS 评价模型,通过计算各评价方案与正、负理想解的贴近度,并对其进行排序,从而确定水资源配置的最佳方案。
1 基于博弈论的TOPSIS 评价模型
1.1 TOPSIS 基本原理
TOPSIS 法是一种逼近于理想解的排序法,它通过欧几里得算法计算各评价目标与正、负理想解之间的差异度,进而计算各评价目标与最优解之间的贴近度,从而选出最优方案[8]。由于TOPSIS 法对评价指标与评价数据没有严格的要求和限制,被广泛应用到各种评价工作中[9]。
TOPSIS 法的基本思想是将评价对象X 与评价标准组成一个矩阵,在对矩阵进行归一化后,确定评价对象内部评价属性的正理想解和负理想解[10]。随后利用欧几里得算法分别计算每一个方案目标与正理想解、负理想解之间的距离,再根据计算得到的正、负理想解计算评价目标与最优值之间的相对贴近度,并对贴近度进行排名,当贴近度越大时,表明该评价目标越接近最优水平。
1.2 计算步骤
(1)设评价对象集合X=(xij)m×n(i=1,2,3,…,m;j=1,2,3,…,n),其中m、n 分别为评价样本个数以及评价指标个数。对评价集合X=(xij)m×n(xij 为第i 个指标在第j 个样本上的实测值)进行归一化处理,得到标准化矩阵C=(cij)m×n,cij 为第i 个指标在第j 个样本上的标准值。对于正向型指标,cij 采用式(1)计算;对于负向型指标,cij 采用式(2)计算。
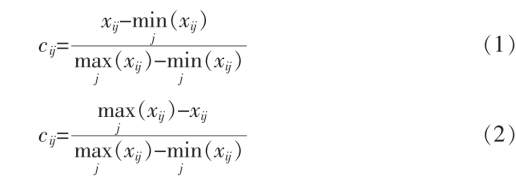
(2)利用博弈论组合赋权法计算指标权重w3。
(3)根据计算得组合权重w3,采用公式(3)建立指标加权矩阵V=(vij)m×n。
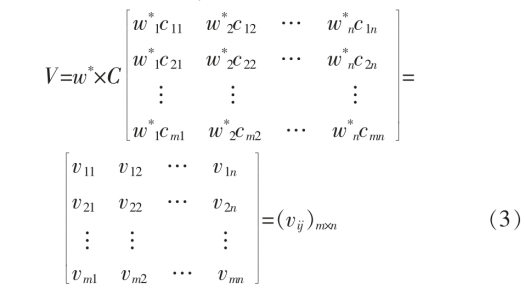
(4)分别采用式(4)和式(5)计算各个评价指标的正理想解x+j 和负理想解x-j。

(7)对相对贴近度按由大到小的方式进行排序,以此作为评价样本的优劣排序。
1.3 博弈论组合权重计算
1.3.1 变异系数法
变异系数法是直接利用各项指标实测值的变异程度来对其进行赋权,计算公式为式(9)和式(10)。

式中:w1j 为第j 个指标的变异系数权重;σj、xj、δj 分别为第j 个指标的标准差、均值、变异系数。
1.3.2 熵权法
熵权法是对指标进行标准化处理后,在计算各指标熵值的基础上,确定其所占权重的计算方法[11]。其计算步骤如下:
(1)对特征矩阵X=(xij)m×n 进行归一化处理,得到标准化矩阵C=(cij)m×n。
(2)通过式(11)和式(12)确定第i 个指标的熵值Hi。
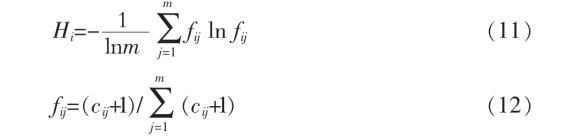
(3)采用式(13)确定第i 个指标的熵权法权重w1j。
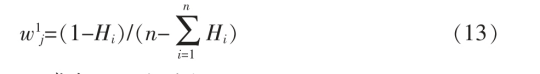
1.3.3 博弈论组合赋权法
博弈论组合赋权法是以纳什均衡为协调目标,寻找不同权重向量集之间的一致和妥协的方法,其集成过程不是简单的物理过程,而是相互比较、相互协调的动态过程[12-13]。博弈论组合赋权的计算步骤如下:

2 模型应用
2.1 数据选取
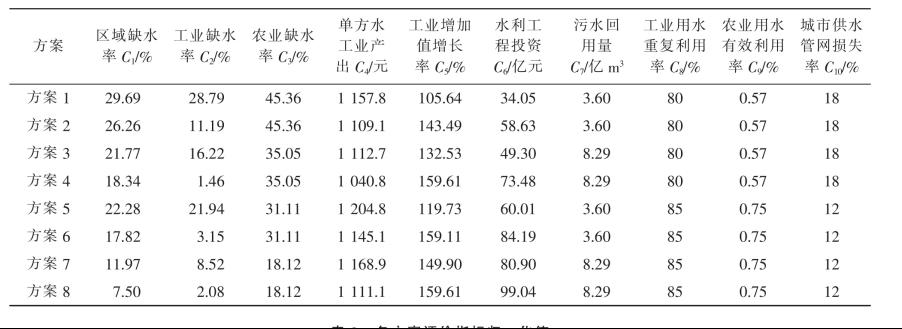
为验证博弈论组合赋权TOPSIS 评价模型在水资源配置方案评价中的可行性,本文选取文献[3]中的案例进行计算。案例中各种水资源配置方案的评价指标值如表1 所示。
表1 各方案评价指标值
Tab.1 Evaluation index value of each scheme
2.2 各评价指标的归一化处理
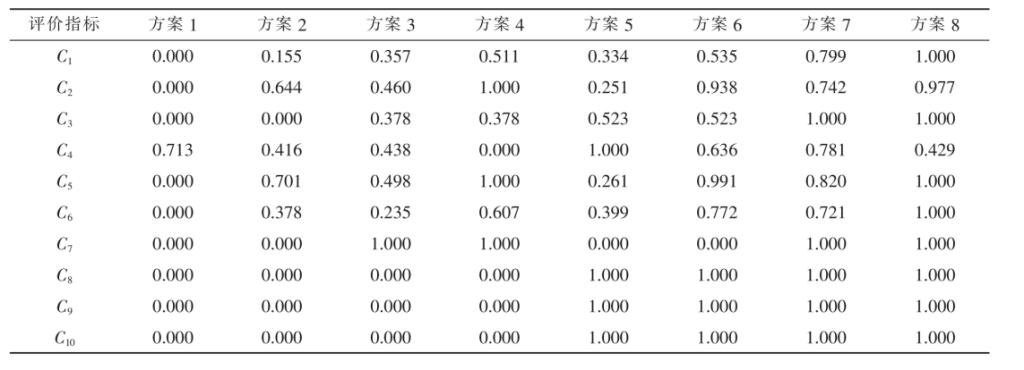
根据式(1)和式(2)对各评价方案指标进行归一化处理,结果如表2 所示。
表2 各方案评价指标归一化值
Tab.2 Evaluation index normalization value of each scheme
2.3 指标权重计算
2.3.1 熵权法权重根据表1 中各方案评价指标数据,应用熵权法求得指标权重w1=(0.060,0.064,0.081,0.047,0.066,0.056,0.156,0.156,0.156,0.156),如图1 所示。
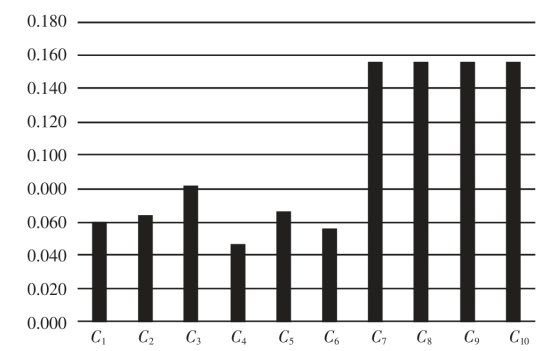
图1 熵权法指标权重
Fig.1 Index weight of entropy weight method
由图1 可以看出,应用熵权法计算评价指标权重,污水回用量C7、工业用水重复利用率C8、农业用水有效利用率C9、城市供水管网损失率C10 在整个评价体系中的重要程度是一样的,单方水工业产出在评价体系中的重要程度最小,具体排序为:C4<C6<C1<C2<C5<C3<C7=C8=C9=C10。
2.3.2 变异系数法权重
采用变异系数法求得的指标权重w2=(0.130,0.299,0.112,0.015,0.050,0.109,0.147,0.011,0.051,0.075),如图2 所示。
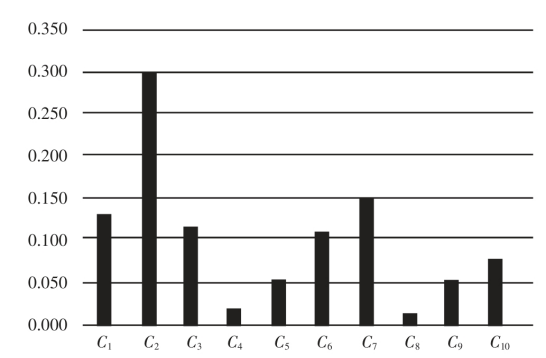
图2 变异系数法指标权重
Fig.2 Index weight of variable coefficient method
由图2 可以看出,通过变异系数法计算权重,工业缺水率C2 在评价体系中所占比重较大,而工业用水重复利用率C8 在评价体系中所占比重较小,具体排序为:C8<C4<C5<C9<C10<C6<C3<C1<C7<C2。
2.3.3 组合权重
根据熵权法和变异系数法求得的评价指标权重w1 和w2,由式(14)~式(16)计算得到组合权重系数a*1=0.391、a*2=0.609,再采用式(17)计算出组合赋权的权重w3=(0.103,0.207,0.100,0.028,0.056,0.088,0.151,0.068,0.092,0.107),如图3 所示。
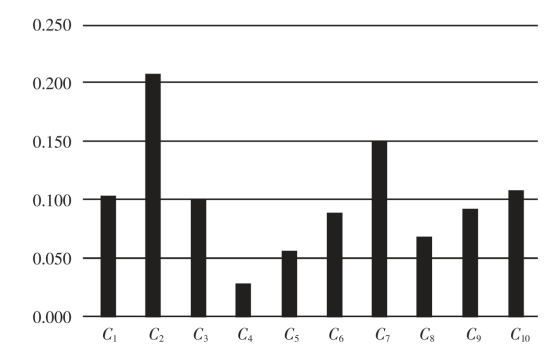
图3 博弈论组合赋权法指标权重
Fig.3 Index weight of combination of game theory and weighting method
由图3 可以看出,根据博弈论组合赋权,工业缺水率C2 在评价体系中所占比重较大,单方水工业产出C4 在评价体系中所占比重较小,具体排序为:C4<C5<C8<C6<C9<C3<C1<C10<C7<C2。
2.3.4 不同赋权法权重值对比
基于熵权法、变异系数法和博弈论组合赋权法求得的评价指标权重值见表3,并根据表3 绘制评价指标权重对比图,如图4 所示。
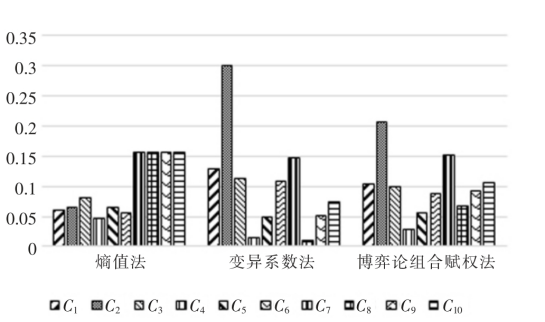
图4 评价指标权重对比图
Fig.4 Comparison of evaluation index weight
表3 各评价指标权重
Tab.3 Weight of each evaluation index
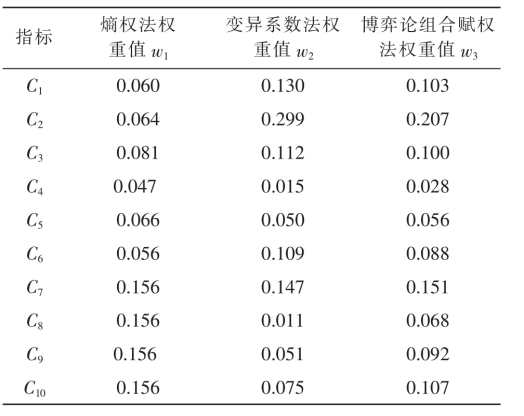
由表3 和图4 可以看出,对水资源配置方案评价影响最大的指标是工业缺水率C2,其次是污水回用量C7,影响最小的指标是单方水工业产出C4。对于不同的赋权法,利用熵权法求得的指标权重过于均衡化,无法判别各项评价指标在评价方案中的重要程度;利用变异系数法求得的指标权重着重反映指标的离散程度。博弈论组合权重结合了熵权法与变异系数法的优点,得到的结果更符合实际情况。
2.4 方案评价
本次选用不同的赋权法对水资源配置方案进行评价。根据式(6)~式(8)分别计算不同赋权法的各方案的正、负理想解距离以及贴近度,计算结果如表4 所示。为了便于比较,将各方案贴近度的计算结果绘制成柱状图,如图5 所示。
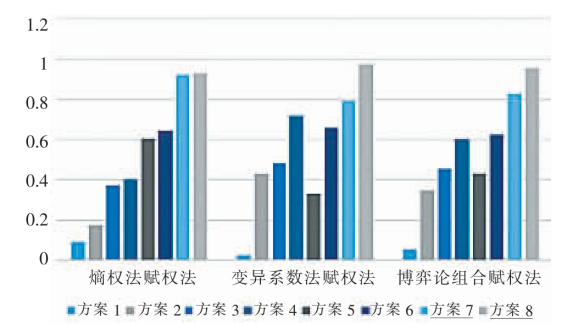
图5 用不同赋权方法计算的各方案的贴近度
Fig.5 The progress of each scheme calculated by different weighting methods
表4 用不同赋权方法计算的各方案的贴近度
Tab.4 The progress of each scheme calculated by different weighting methods
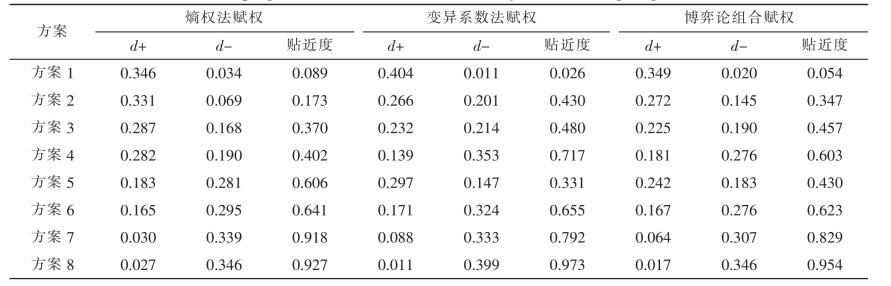
由表4 和图5 可知,基于不同赋权方法的TOPSIS 模型对水资源配置方案的评价结果存在差异。基于熵权法赋权的TOPSIS 模型得到的水资源配置方案优劣排序为:方案8>方案7>方案6>方案5>方案4>方案3>方案2>方案1。基于变异系数法赋权的TOPSIS 模型得到的水资源配置方案优劣排序为:方案8>方案7>方案4>方案6>方案3>方案2>方案5>方案1。基于博弈论组合赋权的TOPSIS 模型得到的水资源配置方案优劣排序为:方案8>方案7>方案6>方案4>方案3>方案5>方案2>方案1。3种模型均得出方案8 为最佳水资源配置方案的结论,但不同赋权方法的模型评价结果有所不同,主要原因在于,变异系数法侧重于反映评价数据的离散程度,不能完全反映评价指标在评价体系中的重要性程度;熵权法侧重于反映评价指标在所有指标中的重要程度,将会影响评价结果的可靠性、准确性;博弈论组合赋权法是利用博弈论辩证思想将变异系数法与秩和比法的权重进行组合,组合权重结合了变异系数法和熵权法的优点,从而使评价结果更贴近区域实际情况。基于博弈论组合赋权的TOPSIS模型得到的水资源配置方案评价结果与吴征等的研究结果基本一致[3]。因此,基于博弈论组合赋权的TOPSIS 评价模型是科学的、合理的。
3 结语
本研究针对以往水资源配置方案评价方法中单一赋权存在的不足,引入博弈论思想,构建了基于博弈论组合赋权的TOPSIS 水资源方案配置评价模型。该模型通过计算各评价方案与正、负理想解的贴近度,选出最佳方案。实例证明,基于博弈论组合赋权求得的评价指标权重吸取、融合了熵权法与变异系数法的优点,使评价结果更贴近实际情况。同时,该评价模型计算简单,是一种科学的、合理的水资源配置方案评价方法。
参考文献:
[1]王 浩,游 进 军.中 国 水 资 源 配 置30 年[J].水 利 学 报,2016,474(3):265-271.
[2]李德良,姜宁.水资源配置方案评价研究进展[J].吉林水利,2022,479(4):42-47.
[3]吴征,吴凤平,沈俊源.基于集对分析法的水资源配置方案综合评价[J].灌溉排水学报,2016,35(12):73-79.
[4]钟平安,张金花,邴建平.基于FIM 赋权的水资源配置方案模糊物元评价[J].水电能源科学,2011,128(4):31-34.
[5]万新宇,郑永路.水资源配置方案多层次可变模糊决策[J].水力发电,2013,475(11):11-15.
[6]张成凤,粟晓玲,蔡焕杰.基于区间层次分析法的榆阳区水资源配置系统和谐性评价研究[J].自然资源学报,2017,32(6):1 053-1 063.
[7]曾国熙,裴源生.黑河流域水资源配置方案合理性评价[J].海河水利,2008(6):1-4.
[8]申毅荣,解建仓.基于熵权和TOPSIS 法的水安全模糊物元评价模型研究及其应用[J].系统工程,2014,32(7):143-148.
[9]TANG Lian,WANG Yongliang,LIU Zixi,et al.TOPSIS Based Assessment of Sustainable Water Resources Utilization[J].Asian Agricultural Research,2018,10(10):63-67.
[10]孙国营,陕振沛,孙新杰,等.基于TOPSIS-灰色关联方法的水资源配置评价模型研究[J].节水灌溉,2019(7):68-71.
[11]李玉兰.基于熵权法的水资源配置综合评价研究[J].河南水利与南水北调,2022,51(9):38-39.
[12]张德彬,刘国东,王亮,等.基于博弈论组合赋权的TOPSIS模型在地下水水质评价中的应用[J].长江科学院院报,2018,35(7):46-50.
[13]朱志强,唐金平,张强,等.基于博弈论组合赋权的正态云模型在地下水水质评价中的应用[J].节水灌溉,2019(6):43-46.
[责任编辑 杨明庆]



